symmetry

Translation is the simplest type of two-dimensional symmetry. It starts with a single motif, or pattern, and repeats this pattern in a straight line by adding motif after motif without overlap. Make a single pattern and then repeat it several times linearly. You are creating a translational symmetrical pattern!

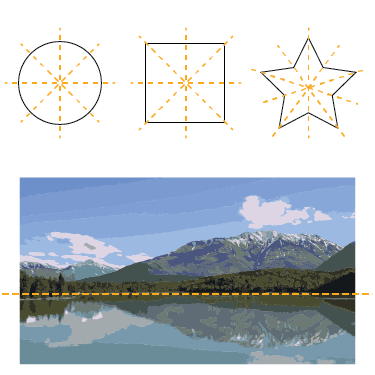
Another easy introduction to symmetry is mirror symmetry. Mirror symmetry is when an object or shape or image or equation ‘mirrors’ or copies itself. Lines of symmetry can be horizontal, vertical and diagonal. Circles and squares divided into two equal parts along a line of symmetry are examples of reflective symmetry. Draw a circle and a square and dot first a vertical and then a horizontal line of symmetry in their geometry. Another example is the reflection of the mountain in a lake. The mountain is the primary object, but the reflection of the mountain is an upside down version of the mountain creating a symmetrical reflection. Sketch a circle and a square showing a mirror symmetry. Then draw a landscape with its reflection on a lake. Reflection symmetry is more dynamic than translation symmetry.

Bilateral symmetry creates similar patterns on either side of a vertical line. In other words, what is on the left of the line is the same as on the right of the line. A vase is an example of bilateral symmetry. The left side of the vessel is the same reflection as the right. Take a look at a butterfly. Find it’s line of symmetry. The left side is a reflection of the right side!

Your face and body are examples of bilateral symmetry. Take a mirror and hold it to the middle of your face at your nose and look into a mirror. You will see what your face would like if both sides were perfectly the same! Better yet, take a photo of your face. Print it and the photo, copy it and into half and flip the image over. Compare a picture of your face with the revised version of your face and see the difference! Asymmetrical symmetry can occur in building plans where the right and left sides of the building hold the same outline, but the inside of the buildings have different sizes and shapes of rooms. Draw an asymmetrical floor plan!

Rotational symmetry occurs when repeated motifs shift around a common point. Take a square piece of paper. Fold the paper in fourth half vertically and horizontally. You should have four equal squares. In the upper right-hand corner create a pattern. Rotate the pattern 90 degrees from the center point and draw it in the lower left. Shift the lower left quadrant 90 degrees to the right and draw this in the lower left quadrant. Complete the 360-degree rotation by rotating the pattern in the lower left 90 degrees to the right and draw it in the upper left. You have created a rotational symmetry!

Glide symmetry introduces more complex combinations than earlier examples of symmetry. Glide symmetry is when a motif or pattern is translated (copied linearly) and reflected. Try taking a stepped two square motif with the second square’s top edge lined up with the first squares middle line. You can fill these stepped squares with any patterns.

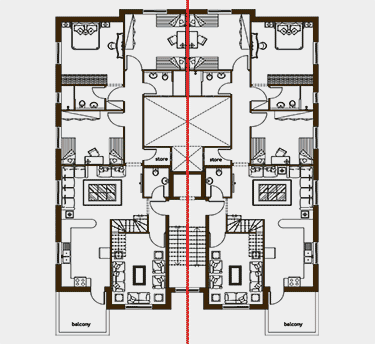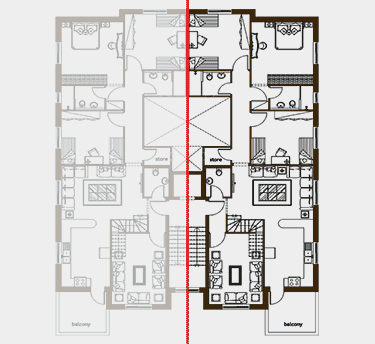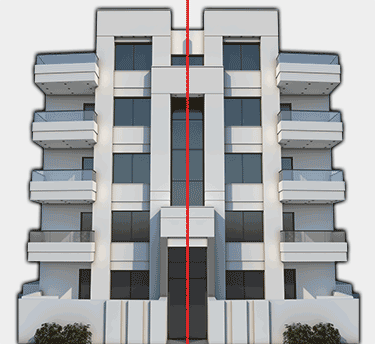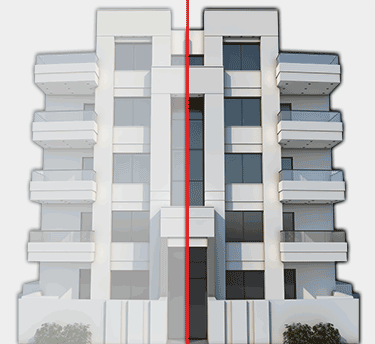
Think balance. Think parts to whole, top to bottom, inside to outside. Architecture can express symmetry in its plan, elevation, layout and site plan. When architecture expresses symmetry, it suggests experiences and contemplation of balance. Explore definitions of the word balance. Try to look at buildings and see if they are “balanced”. Can imbalance suggest balance? Define visaul symmetry in architecture and take photos of buildings which appear balanced and static; contrast them with symmetrical buildings or buildings that are dynamic. Label your photos Symmetrical/Balance and Dynamic/Movement. How do these different approaches make you feel?